Abstract
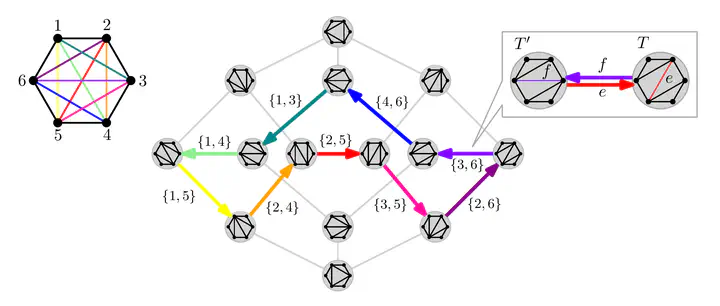
The flip graph of triangulations has as vertices all triangulations of a convex n-gon, and an edge between any two triangulations that differ in exactly one edge. An r-rainbow cycle in this graph is a cycle in which every inner edge of the triangulation appears exactly r times. This notion of a rainbow cycle extends in a natural way to other flip graphs. In this paper we investigate the existence of r-rainbow cycles for three different flip graphs on classes of geometric objects: the aforementioned flip graph of triangulations of a convex n-gon, the flip graph of plane trees on an arbitrary set of n points, and the flip graph of non-crossing perfect matchings on a set of n points in convex position. In addition, we consider two flip graphs on classes of non-geometric objects: the flip graph of permutations of 1,2,…,n and the flip graph of k-element subsets of 1,2,…,n. In each of the five settings, we prove the existence and non-existence of rainbow cycles for different values of r, n and k.
A preliminary version was presented at the International Symposium on Computational Geometry (SoCG'18).