Abstract
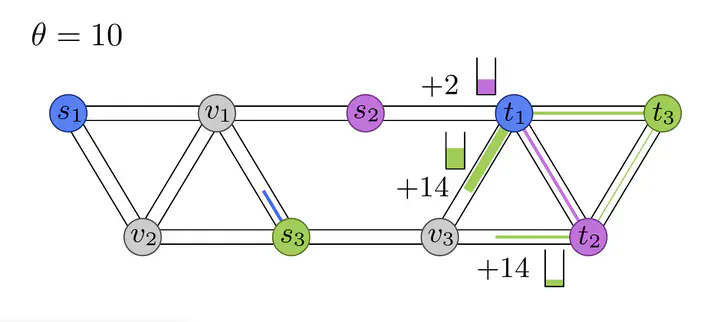
We study dynamic network flows and introduce a notion of instantaneous dynamic equilibrium (IDE) requiring that for any positive inflow into an edge, this edge must lie on a currently shortest path towards the respective sink. We measure current shortest path length by current waiting times in queues plus physical travel times. As our main results, we show: 1. existence and constructive computation of IDE flows for single-source single-sink networks assuming constant network inflow rates, 2. finite termination of IDE flows for multi-source single-sink networks assuming bounded and finitely lasting inflow rates, 3. the existence of IDE flows for multi-source multi-sink instances assuming general measurable network inflow rates, 4. the existence of a complex single-source multi-sink instance in which any IDE flow is caught in cycles and flow remains forever in the network.