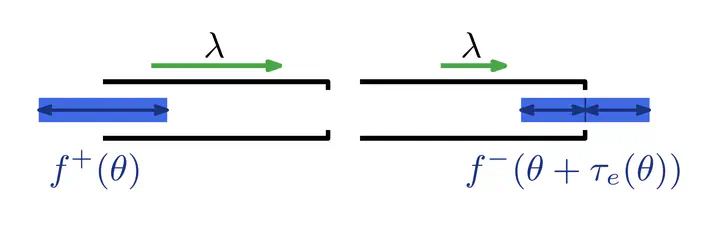
Abstract
Predicting selfish behavior in public environments by considering Nash equilibria is a central concept of game theory. For the dynamic traffic assignment problem modeled by a flow over time game, in which every particle tries to reach its destination as fast as possible, the dynamic equilibria are called Nash flows over time. So far, this model has only been considered for networks in which each arc is equipped with a constant capacity, limiting the outflow rate, and with a transit time, determining the time it takes for a particle to traverse the arc. However, real-world traffic networks can be affected by temporal changes, for example, caused by construction works or special speed zones during some time period. To model these traffic scenarios appropriately, we extend the flow over time model by time-dependent capacities and time-dependent transit times. Our first main result is the characterization of the structure of Nash flows over time. Similar to the static-network model, the strategies of the particles in dynamic equilibria can be characterized by specific static flows, called thin flows with resetting. The second main result is the existence of Nash flows over time, which we show in a constructive manner by extending a flow over time step by step by these thin flows.